The Graph–Fibrations Home Page
The purpose of this page is discuss the definition of a particular kind of graph morphism that has found application in several different fields of mathematics and computer science. Since the idea has been rediscovered several times by different people, it is useful to have a single place where all definitions are compared.
An effort has been made to compare results and to track the oldest definitions. If you find a mistake in the attribution, or missing references, please write me.
Preliminaries
A graph G is given by a set of nodes NG, by a set of arcs AG, and by source and target functions sG: AG→NG and tG: AG→NG that specify the source and the target of each arc. The subscripts will be dropped when no confusion can arise. In the finite case, we usually write n for the number of nodes and m for the number of arcs.
A graph (homo)morphism φ: G→H is given by two functions (ambiguously denoted by the same symbol) φ: NG→NH and φ: AG→AH which commute with source and target: that is, tH∘φ = φ∘tG and sH∘φ = φ∘sG.
Fibrations
Each graph G generates freely a category G* that has the nodes of G as objects, and the paths of G as arrows (composition is concatenation, and the empty paths pointed at each node are the identities). Given a graph morphism φ: G→B, the free category functor gives a functor φ*: G*→B*. We say that φ is a graph fibration when φ* is a fibration (see, e.g., Francis Borceux, “Handbook of Categorical Algebra 2”, volume 51 of the Encyclopedia of Mathematics and Its Applications, Cambridge University Press, 1994). The definition of categorical fibration is credited to Grothendieck (“Technique de descente et théorémes d'existence en géométrie algébrique, I. Généralités. Descente par morphismes fidélement plats”, Seminaire Bourbaki, 190, 1959‒1960).
An elementary definition of fibration can be easily derived: φ: G→B is a fibration iff for every arc a of B and every node x of G such that φ(x) = t(a) there exist a unique arc ax of G satisfying φ(ax) = a and t(ax) = x. The graph G is the total graph of the fibration, and B is its base. The set of nodes of G mapped to a node x of B is called the fibre over x.
The property defining fibrations is called the lifting property: each arc of B can be
uniquely lifted along
the fibre of its target. The figure on the left 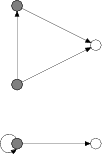
 shows two
graphs and a morphism specified implicitly by the colours on the nodes. The morphism is not a fibration
because the loop on the grey node lacks a lifting, and the other arc has too many. The figure
on the right shows a fibration, instead.
shows two
graphs and a morphism specified implicitly by the colours on the nodes. The morphism is not a fibration
because the loop on the grey node lacks a lifting, and the other arc has too many. The figure
on the right shows a fibration, instead.
Note that by repeating the lifting for all arcs coming into a node x of B, we obtain a local in-isomorphism—a bijection between the in-neighbourhood of x and that of every y in the fibre of x.
Dually, an opfibration has the property that each arc of B can be uniquely lifted along the fibre of its source.
The connection with categorical fibrations was noted (and, in fact, used as a definition) by Paolo Boldi and Sebastiano Vigna in “Fibrations of Graphs” (Discrete Math., 243:21‒66, 2002), but the elementary definition appears several times in previous literature with different names. Grothendieck's definition is however the oldest appearance of the idea (albeit in a very general form); the definition was, in turn, inspired by the topological definition of fibration (from which terms such as “fibre”, “total graph” and “base” are derived).
Two important concepts about fibrations are the universal total graph at x—the unique largest in-tree fibred over G whose root is mapped to x—and the minimum base—the smallest graph over which G can be fibred. They are strictly linked, as the universal total graphs of the minimum base are all distinct but, as a set, they are equal to the universal total graphs of G. The minimum fibration base is fibration prime, that is, it cannot be fibred nontrivially and epimorphically.
In fact, the universal total graph and the minimum base are almost ubiquitous concepts—even in situations where there is no explicit notion of fibration. Typical examples are the unfolding of a nondeterministic automaton (appearing, e.g., in concurrency theory), and the minimisation of a sofic system (a particular kind of finite-state automaton—see below).
We note that it is immediate to prove by lifting that an (op)fibration with strongly connected base is epimorphic (i.e., both the node and arc components are surjective). Because of this fact, in some context (op)fibrations have been directly defined as epimorphisms; however, there is no need for such a restriction, as most of the relevant results can be proved without this additional condition. In symbolic dynamics, for instance, it is often assumed that all nodes have strictly positive indegree and outdegree: again, the theory of graph (op)fibrations can be developed without such assumptions.
Several properties of factor maps proved in the context of symbolic dynamics have interesting categorical counterparts. For instance, Masakazu Nasu proved that if the functor φ*: G*→B* has bounded fibres (in dynamicspeak, it must be uniformly finite-to-one) the characteristic polynomial of B divides that of G and the maximum eigenvalue is the same (“Uniformly finite-to-one and onto extensions of homomorphisms between strongly connected graphs”, Discrete Math., 39(2):171-197, 1982).
Connections with Topological Graph Theory
A graph morphism that is both a fibration and an opfibration is a covering. In this case, the whole neighbourhood of x and that of every y in the fibre of x are in bijection.
The connection with the more standard, topological notion of graph covering on undirected graphs is immediate once undirected graphs are represented as directed graphs endowed with an involution β satisfying β∘t = s (which implies β∘s = t). The involution identifies arcs in opposite directions, and each orbit of the involution is identified with an undirected arc. Now a covering (as defined above) preserving involutions is exactly a topological graph covering.
Indeed, using the definition of covering given above solves the rather subtle issues determined by the presence of loops: for instance, a symmetric graph with one node and two loops has the bidirectional line as universal symmetric covering, but the universal symmetric covering projection is different depending on whether the symmetry is the identity or not; moreover, when only one loop is present the universal symmetric covering reduces to a single bidirectional segment, which accounts for the “loops counted once vs. loops counted twice” dilemma in the definitions found in the literature. Some elaboration on this topic can be found in “Fibrations of Graphs”.
Divisors and Spectrum
The community working on spectra of graphs (e.g., to the study of the eigenvalues of the adjacency matrices of graphs) defined in the sixties the concept of graph (front) divisor (in German, Teiler). A graph D is a front divisor of G if it is possible to build a map f: NG→NB so that the number of links going from a node a node x of G to all nodes in f‒1(z) is equal to the number of links going from f(x) to z. The raison d'être of divisors is that if D is a divisor of G the characteristic polynomial of D divides that of G.
It is immediate that the existence of an opfibration from G to D exhibits D as a front divisor of G (the same hold for rear divisors and fibrations). However, (op)fibrations have a richer structure, as they comprise also a map on the arcs. One could say that (op)fibrations are to divisors as functions are to partitions of the integers. Indeed, many results about graph divisors extends immediately to (op)fibrations (for instance, every group acting on a graph induces a fibration and an opfibration). See the encyclopedic book “Spectra of Graphs”, by Dragoš M. Cvetković, Michael Doob and Horst Sachs (Academic Press, 1980), and its extended bibliography.
Note that lacking a direct definition of (op)fibration, the connection with graph morphism was observed in a different way by Horst Sachs in his paper “Simultane Überlangerung gegebener Graphen” (Magyar Tud. Akad. Mat. Kutató Int. Közl., 9:415‒427, 1965): if G covers B (in the classical undirected sense) then the characteristic polynomial of B divides that of G.
Actually, even more is true: given a fibration φ: G→B and a vector x indexed by B, define the (right) lifting of x along φ, denoted xφ, by (xφ)i = xφ(i) (essentially, we copy the components of x along each fibre). If x is an eigenvector of B, then xφ is an eigenvector of G for the same eigenvalue.
Symmetrically, if x is a vector indexed by G define the (left) lowering of x along φ, denoted φx, by adding up the values of x along each fibre. If x is an eigenvector of G and φx is not zero, then φx is an eigenvector of B for the same eigenvalue.
These results induce a number of relationships between the eigenvalues and eigenvectors of two graphs related by a fibrations (dual results exists for opfibrations). Note however that the abovementioned results by Masakazu Nasu show that divisibility of characteristic polynomials is provable under weaker conditions, as if φ is an (op)fibration φ* has bounded fibres, but there are graph morphisms inducing free functors with bounded fibres that are not a composition of (op)fibrations, as shown by Bruce Kitchens in his Ph.D. thesis and reported by Bruce Kitchens, Brian Marcus, and Paul Trow in “Eventual factor maps and compositions of closing maps”, Ergodic Theory Dynam. Systems, 11(1):85-113, 1991.
Equitable Partitions and Graph Isomorphism
Several people in the 60's and 70's developed algorithms for graph isomorphism or tests for graph isomorphism starting from the construction of the minimum base of the graph (or the minimum opfibration base). The oldest known explicit mention of the procedure appears in Stephen H. Unger's program for graph isomorphism (“GIT—A Heuristic Program for Testing Pairs of Directed Line Graphs for Isomorphism”, Comm. ACM, 7(1):26‒34, 1964), where it is called the Extend method. Building on that result, a further refinement was proposed (always starting from a minimum base) by D.G. Corneil and C.C. Gotlieb in “An Efficient Algorithm for Graph Isomorphism” (Journal of the ACM, 17:51‒64, 1970).
A. Cardon and Maxime Crochemore (“Partitioning a Graph in O(|A| log2 |V|)”, Theor. Comput. Sci., 19:85‒98, 1982) proposed a very efficient computation of the minimum base by exploiting some ideas appeared in Hopcroft's minimal-automaton algorithm (“An n logn Algorithm for Minimizing States in a Finite Automaton”, in Theory of Machines and Computation, Academic Press, 1971). They claim an O(m logn) time bound, albeit the actual bound is O((m+n) logn).
Independently from this computer-science related line of development, Boris Weisfeiler and Andrei Leman proposed a reduction of a graph to “canonical form” that is just the minimum base. (“The reduction of a graph to canonical form and the algebra which appears therein”, in Nauchno-Technicheskaya Informatsia, 2(9):12–16, 1968; english translation by G. Ryabov). The name seem to imply that isomorphism between graphs could be decided using isomorphism between minimum bases, and indeed Conjectures 1 and 2 in the paper would lead to that conclusion, but this is not the case (the Weisfeiler–Leman canonical form and its extensions have become recently very popular in the literature about graph neural networks).
In a further independent development, mathematicians have been studying the concept of equitable partition, that is, a partition of the node set that satisfies a requirement equivalent to that of front divisors: the number of vertices of part C adjacent to a vertex x must depend only on the part of x. The concept has been introduced by Allen J. Schwenk in “Computing the Characteristic Polynomial of a Graph” (Graphs and Combinatorics, volume 406 of Lecture Notes in Mathematics, 153‒172. Springer–Verlag, 1974). The fact that equitable partitions and divisors were actually the same concept, however, went apparently unnoticed for some time, as well as the connection with graph isomorphism and the Weisfeiler–Leman paper.
Brendan McKay used coarsest equitable partitions as a starting point for its graph-isomorphism program nauty (actually, nauty is much more, as it can compute automorphism groups and canonical labellings). The coarsest equitable partition gives exactly the fibres of the minimum base, and McKay describes in his Ph.D. thesis (1975) a partitioning algorithm that is just slightly less efficient (O(n2 logn)) than that of Cardon and Crochemore (“Practical Graph Isomorphism”, Congressus Numerantium, 30:45‒87, 1981).
Both algorithms refine the current partition using a subset of parts; the main difference is in the way this subset of parts is handled—Cardon and Crochemore use the subset to compute directly a refinement in one shot, whereas McKay puts the parts in the subset in a queue and uses them one at a time to build a refinement. The former process lends itself to a tighter analysis, giving a better bound, but the latter may in principle converge more quickly to the result. The two approaches were merged in a coloured version proposed by Paolo Boldi, Violetta Lonati, Massimo Santini and Sebastiano Vigna in “Graph fibrations, graph isomorphism, and PageRank” (RAIRO Inform. Théor., 40:227‒253, 2006) and working in time O(n logn + m log(n+m+c) logn), where c is the number of colours. The latter algorithm is oriented towards very large graphs and requires no data structure—just n vectors containing overall m integers and six vectors of n integers each.
Fibrations and Distributed Systems
If a graph is used to represent the structure of a network exchanging messages, and the processors of the network execute the same algorithm starting from the same initial state, the existence of a fibration φ: G→H implies that, whatever algorithm is used, there are executions in which the behaviour of the nodes in G is fibrewise constant (i.e., all processors in the same fibre are always in the same state). Besides providing easy impossibility results, further study provided the effective solution of the distributed computation problem: given a set of networks, a set of communication primitives and a problem (expressed as a relation between inputs and outputs), is there an algorithm solving the problem on all the given networks? Using fibrations it is possible to provide a characterisation that is effective when the set of networks and the problem are finite: that is, there is an algorithm that outputs either a distributed algorithm for the problem, or an impossibility result. Analogous strong results were proved for a class of self-stabilising systems.
The usage of graph homomorphisms to prove impossibility results, of course, is not new and started with Dana Angluin's seminal paper “Local and global properties in networks of processors” (Proc. 12th Symposium on the Theory of Computing, pages 82‒93, 1980), in which it is shown that the existence of a covering projection from a network to a smaller network implies impossibility of election in an interleaved model with bidirectional communication. The application of graph-theoretical ideas developed in a number of papers (most notably those by Yamashita and Kameda), but it was the application of fibrations that made it possible to prove effective results for a very wide range of models (and, for the first time, for unidirectional communication models).
The application to distributed systems required some new results: most notably, Nancy Norris' proof that two universal coverings of the same finite graphs are isomorphic iff they are isomorphic up to level n−1 (“Universal covers of graphs: Isomorphism to depth n−1 implies isomorphism to all depths”, Discrete Appl. Math., 56:61‒74, 1995), which was easily extended to universal total graphs by Boldi and Vigna, and the even tighter result that n+D levels (where D is the diameter) of any universal total graph of a strongly connected fibration-prime graph uniquely identify the latter (see again “Fibrations of graphs”).
The researchers working in distributed systems were not aware of the body of knowledge gathered by the community working on symbolic dynamics (see below), so some results were reproved from scratch.
Semicovers
Working on the spectra of trees, P. Híc, Roman Nedela and S. Pavlíková have previously defined in their 1992 paper “Front-Divisors of Trees” (Acta Math. Univ. Comenianae, LXI(1), 1992, pp. 69‒84) the notion of semicovering projection (in our terminology, opfibration), and applied it to the symmetric representation of undirected trees. In particular, they notice the relation with divisors and propose a functional voltage representation. The representation has been reintroduced independently in “Fibrations of Graphs” and extended to a categorical equivalence between the category of fibrations over B and the category of presheaves on B*. The authors prove also several theorems about the interplay between the automorphism group and front divisors. Some of the results apply only to trees, however (e.g., the minimum base turns out to be the quotient by the automorphism group, which is not true in general).
Symbolic Dynamics and One–Sided Coverings
The community working on symbolic dynamics and coding has used (op)fibrations in several ways for a long time under the name of (right) left coverings. The encyclopedic book “An Introduction to Symbolic Dynamics and Coding”, by Douglas Lind and Brian Marcus (Cambridge University Press, 1995) collects the large amount of knowledge gathered in the field. Some results proved in “Fibrations of Graphs” in a categorical settings appear here, albeit usually with some additional hypothesis. We will try to briefly highlight the main connections.
A sofic shift is a shift formed by the biinfinite paths of an arc-labelled graph (the graphs considered are usually strongly connected, a.k.a. irreducible). From an automaton-theoretic viewpoint, it is an automaton all whose states are initial and final. Right-resolving presentations of a sofic shift correspond to deterministic automata, and the Fischer cover of a right-resolving sofic shift is the smallest such presentation—the minimum deterministic automaton (recognising the same language). Because of the fact that all states are initial and final, the minimum deterministic automaton, however, is exactly the minimum opfibration base (a dual correspondence relates left-resolving presentations and covers with fibrations). Note that since the involved graphs are deterministic, the theory is radically simplified—you don't need universal total graphs and all the rest, because the language recognised starting at a node x is sufficient to identify nodes with the same universal total graph (the point of the Fischer cover is precisely that the language recognised starting at any two nodes is different—in fibrationspeak, primality). The original definition was restricted to strongly connected graphs, but has been extended by Wolfgang Krieger to general graphs (“On sofic systems. I”, Israel J. Math., 48(4):305‒330, 1984). Again, these differences are immaterial in the development of fibration theory, as it uses general graphs (in fact, not even necessarily finite).
Of course, all algorithms developed for graph partitioning and isomorphism can be used to compute the Fischer/Krieger covers in a very efficient way.
Roy L. Adler and Brian Marcus in the treatise “Topological entropy and equivalence of dynamical systems” (volume 20 of Mem. Amer. Math. Soc., 1979), define (right-) left-resolving maps (Definition 3.31) between shifts of finite type. The definition is given in terms of the 0-1 matrices that induce the shifts, and if we interpret them as graphs we obtain in nuce the definition of an (op)fibration. There are a number of additional hypothesis on the matrices, however, and the definition is not given for general graphs (the matrices are 0-1, so there are no parallel arcs).
Shortly thereafter, Masakazu Nasu defined (backward-) regular graph homomorphisms (“Constant-to-one and onto global maps of homomorphisms between strongly connected graphs”, Ergodic Theory Dynam. Systems, 3(3):387‒413, 1983), which are exactly (fibrations) opfibrations; Nasu refers to them as equivalent to the right/left-resolving maps defined by Adler and Marcus, but actually his graphs are more general (albeit finite), and the definition he gives is exactly that of unique lifting along a fibre.
Finally, the definition of (right) left covering given in “An Introduction to Symbolic Dynamics and Coding” is identical to that of (op)fibration.
Williams (“Classification of Subshifts of Finite Type”, Ann. of Math., 98:128‒153, 1973) introduced the notions of subdivision and amalgamation matrices, which can be used as a substitute of left/right-coverings. Williams introduced also the notions of state splitting and state merging, which when applied to a graph G roughly correspond to building a graph fibred over G or a graph over which G can be fibred, respectively.
The Categorical Side
Some theorems about categorical (op)fibrations can be extended or translated into theorems about graph (op)fibrations. Most importantly, there is a categorical equivalence between presheaves over G* and the category of fibrations into G. The equivalence extends to the case of fibrations the notion of voltage assignment (Jonathan L. Gross and Thomas W. Tucker, “Generating all graph coverings by permutation voltage assignments”, Discrete Math., 18(3):273‒283, 1977). The representation of a fibration as a presheaf over G* gives, for each arc of G, a function (the restriction) that describes how arcs are lifted; the function is a bijection in the case of coverings, and corresponds essentially to a coordinate-free voltage assignment.
Pullbacks of (op)fibrations are (op)fibrations. From this result (and using the classification of coverings of bouquets) it is easy to show that finite regular directed graphs of the same degree have a finite common cover. More results can be found in “Fibrations of Graphs”.